画像処理
ビュフォンの針を画像解析を使って計算してみよう!
はじめまして、2年目社員のAです。 蒸し暑い日が続いていますね。学生の皆さんは夏休みが待ち遠しい時期だと思います。 突然ですが、針の長さや本数から円周率を求められることを知っていますか? 今回は弊社の画像解析ソフトウェア「WinROOF」シリーズを使用して、円周率を求めてみました!
円周率とは
円周率とは、円の周りの長さと円の直径の比、つまり円周÷直径のことです。
円が大きくなっても、小さくなっても円周率は同じ値になります。
円周率は割り切れない数字で、小数がずっと続くので、よく3.14として計算に使われたり、π(パイ)と表されたりします。
ビュフォンの針とは
ビュフォンの針は、等間隔の平行線が引かれた平面に針を投げたときの、針が線と交わる確率を求める数学の問題です。この確率から円周率を求めることができます。

■計算してみよう
例えば、こちらの画像の場合、散らばった12本の綿棒(針)のうち、フローリングの線(等間隔の平行線)と交わる綿棒は9本あります。
ということは、フローリングの線に綿棒がぶつかる確率は12本中の9本、すなわち、9÷12=0.75となりますね。
綿棒の本数をN、そのうちフローリングの線と交わった本数をnとすると、確率はn/Nと表すことができます。
実はこのとき、綿棒の長さをL、フローリングの線の間隔をDとすると、針と線が交わる確率は2L/πDとなります!
これは、フローリングの線の間隔(D)が綿棒の長さ(L)以上に広い場合に成り立ちます(L≦D)。
(なぜそうなるの?と詳しく知りたい方は「ビュフォンの針」で調べてみてください。)
すなわち、以下の式が成り立ちます。
2L/πD=n/N
綿棒の長さL:7.1cm、フローリングの線の間隔D:7.35cmであるため、
先ほどの式に代入してみると、
2×7.1÷7.35π=9÷12
π=(2×7.1×12)/(7.35×9)=2.576...
より円周率は2.58となります。
円周率って3.14ですよね。
誤差が大きいのは、綿棒を12本しか投げていないからです。
たくさん投げるほど誤差が小さくなります。
でも本数が多くなると、交わった本数を目で見て数えるのは大変。
途中で数え間違えたり、記録を忘れたりしてしまうかもしれません。
■画像解析で計算してみよう
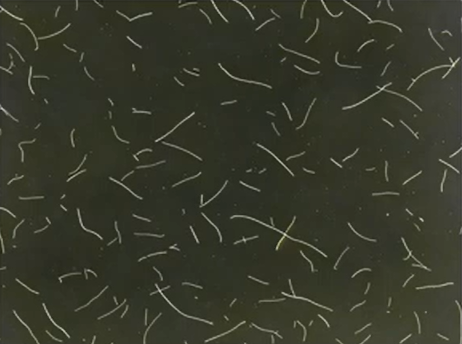
そこで今回は、綿棒12本を10回投げて、画像処理を用いて数えてみました。
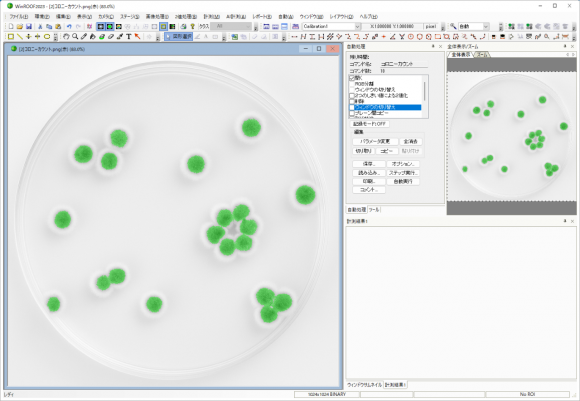
弊社の画像解析ソフトウェア「WinROOF」シリーズでは画像処理を設定すれば、自動で計測が可能です。
それでは「WinROOF」を使用してフローリングの線と綿棒の交点を数えてみましょう。
① 綿棒を抽出します。

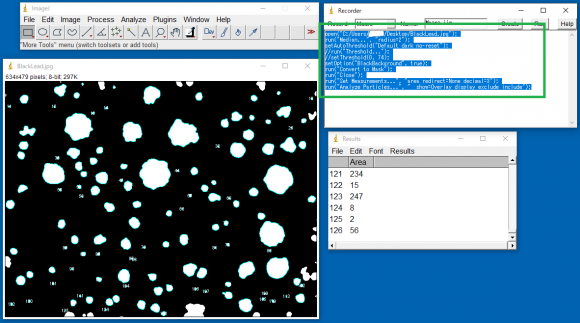
② フローリングの線を抽出します。

③ ①と②の重なった箇所(論理積)から交点を抽出します。

④ ①~③を10回分の画像で繰り返し処理します。
「WinROOF」では計測結果をまとめて出力することが可能です。

今回はフローリングの線と交わった綿棒は平均7.1本でした。改めて、円周率を計算してみます。
綿棒の長さL:7.1cm
フローリングの線の間隔D:7.35cm
綿棒の本数N:12本
線と交差した綿棒の本数n:7.1本
2L/πD=n/Nに代入して計算してみると、
2×7.1÷7.35π=7.1÷12
π=(2×7.1×12)/(7.35×7.1)=3.265...
より円周率は3.27となります。
画像1枚のときより、実際の円周率3.14との誤差が小さくなりました。
中学生の学習範囲でも取り組める面白い実験ですので、夏休みの自由研究のテーマにするのも良いかもしれませんね!
家にあるものでも簡単にできます!
ぜひ投げる場所や投げるモノを変えて試してみてください!
WinROOFシリーズの特徴
いかがでしたか。ビュフォンの針の問題だけでなく、「WinROOF」では顕微鏡、デジタルカメラ、スマートフォンなどで撮影した画像を解析することができます。
複数枚の画像を一気に解析したり、解析結果をExcelやCSVへレポート出力したりすることが可能です。
最後まで読んでいただき、ありがとうございました。
画像解析にご興味がありましたら、お気軽にお問合せください。
■■三谷商事ビジュアルシステム部への問い合わせはこちらをクリック!■■